矩阵与向量¶
如果$m$和$n$是正整数,那么$m \times n$矩阵有如下形式
$$ \left[\begin{array}{rrrrr} a_{11} & a_{12} & a_{13} & \ldots & a_{1 n} \\ a_{21} & a_{22} & a_{23} & \ldots & a_{2 n} \\ a_{31} & a_{32} & a_{33} & \ldots & a_{3 n} \\ \vdots & \vdots & \vdots & & \vdots \\ a_{m 1} & a_{m 2} & a_{m 3} & \ldots & a_{m n} \end{array}\right] $$其中矩阵的每一项 $a_{ij}$是一个数字。一个$m \times n$矩阵有$m$行和$n$列。矩阵通常用大写字母表示。

特殊矩阵¶
- 行向量 $1 \times n$矩阵 $$\begin{bmatrix}3 & 7 & 2 \end{bmatrix}$$
- 列向量 $n \times 1$矩阵 $$\begin{bmatrix}4 \cr 1 \cr 8 \end{bmatrix}$$
方阵(Square vector) $n \times n$矩阵 $$\begin{bmatrix}9 & 13 & 5 \cr 1 & 11 & 7 \cr 2 & 6 & 3 \end{bmatrix}$$
对角矩阵(Diagonal matrix) $$A = \begin{bmatrix}\begin{matrix}\lambda_1 & 0 \\ 0 & \lambda_2 \end{matrix} & \text{0} \\ \text{0} & \begin{matrix}\ddots & 0 \\ 0 & \lambda_n \end{matrix} \end{bmatrix}$$
$A = diag(\lambda_1, \lambda_2, \cdots, \lambda_n)$
单位矩阵(Identity matrix) $$I_n = \begin{bmatrix}\begin{matrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} & \begin{matrix}\cdots & 0 \\ \cdots & 0 \\ \cdots & 0 \end{matrix} \\ \begin{matrix}\vdots & \vdots & \vdots \\ 0 & 0 & 0 \end{matrix} & \begin{matrix}\ddots & 0 \\ 0 & 1 \end{matrix} \end{bmatrix}$$
$I_n = diag(1, 1, \cdots, 1)$零矩阵(Zero matrix) $$O = \underbrace{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}}_{2 \times 3 \ zero \ matrix}$$
矩阵加法和标量乘法( Addition and Scalar Multiplication)¶
加法¶
如果 $A = [a_{ij}]$, $B = [b_{ij}]$ ,且二者都为 $m \times n$矩阵, 那么它们的和为$m \times n$ matrix given by
$$ A + B = [a_{ij} + b_{ij}] $$只有行列数分别相等的矩阵才可作加法。
$$ \begin{bmatrix}-1 & 2 \\ 0 & 1 \end{bmatrix} + \begin{bmatrix}1 & 3 \\ -1 & 2 \end{bmatrix} = \begin{bmatrix}-1+1 & 2+3 \\ 0+(-1) & 1+2 \end{bmatrix} = \begin{bmatrix}0 & 5 \\ -1 & 3 \end{bmatrix} $$ $$ A-B=A+(-1)B $$数乘¶
如果 $A=[a_{ij}]$ 是一个 $m \times n$的矩阵,$c$ 是一个标量, 那么矩阵 $A$ 与$c$的数乘是 $m \times n$ 矩阵,有
$$ cA=[ca_{ij}] $$ $$ A=\begin{bmatrix}2 & 2 & 4 \\ -3 & 0 & -1 \\ 2 & 1 & 2\end{bmatrix} \quad 3A=3\begin{bmatrix}2 & 2 & 4 \\ -3 & 0 & -1 \\ 2 & 1 & 2\end{bmatrix} $$矩阵加法与数乘的性质¶
$A$, $B$, $C$ 为 $m \times n$ 矩阵, $c$ 和 $d$ 是标量。
- $A+B=B+A$ 交换律(Commutative Property of Matrix Addition)
- $A+(B+C)=(A+B)+C$ 结合律(Associative Property of Matrix Addition)
- $(cd)A=c(dA)$ 数乘结合律(Associative Property of Scalar Multiplication)
- $1A=A$ Scalar Identity Property
- $c(A+B)=cA+cB$ 分配律(Distributive Property)
- $(c+d)A=cA+dA$ 分配律(Distributive Property)
矩阵运算¶
矩阵乘法¶
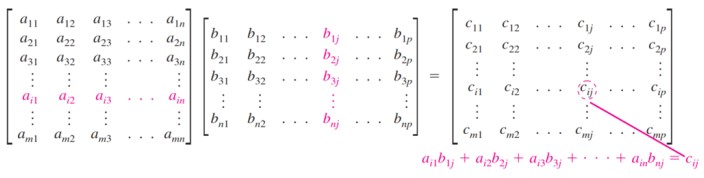
如果 $A=[a_{ij}]$ 是 $m \times n$ 矩阵且 $B=[b_{ij}]$ 是一个 $n \times p$ 矩阵, $AB$ 是 $m \times p$ 矩阵 $$AB=[c_{ij}]$$ where $c_{ij}=a_{i1}b_{ij}+a_{i2}b_{2j}+a_{i3}b_{3j}+\cdots+a_{in}b_{nj}$.
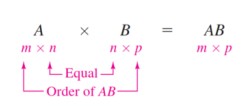
矩阵乘法的运算性质¶
设 $A$, $B$, $C$ 是矩阵, $c$ 是一个标量.
- $A(BC)=(AB)C$ 矩阵乘法的结合律(Associative Property of Matrix Multiplication)
- $A(B+C)=AB+AC$ 矩阵乘法的分配律(Distributive Property)
- $(A+B)C=AC+BC$ 矩阵乘法的分配律(Distributive Property)
- $c(AB)=(cA)B=A(cB)$ 与标量乘法的结合律(Associative Property of Scalar Multiplication)
矩阵的转置(Matrix Transpose)¶
在线性代数中,一个矩阵的转置是一个算子,它使一个矩阵关于它的对角线上翻转,也就是说,它通过产生另一个矩阵来交换矩阵的行和列指标$A^T$ 也写为 $A'$, $A^{tr}$, $^{t}A$ 或 $A^t$).
矩阵转置的性质¶
- $(A^T)^T=A$
- $(A+B)^T=A^T+B^T$
- $(AB)^T=B^TA^T$
- $(cA)^T=cA^T$