什么是数学建模?
模型与数学模型
所谓模型就是采用某种形式来近似地描述或模拟所研究的对象或过程的一种结构. 模型大体可分为两类:实物模型 (具体模型) 和理论模型(抽象模型).
实物模型与理论模型
实物模型又可以分为模拟模型和缩尺 (肖像) 模型两种.
模拟模型是用其他现象或过程来描述所研究的现象或过程,用模型性质代表原来的性质. 例如, 可用电流模拟热流、流体的流动, 用流体系统模拟车流等.
模拟模型可再分成直接模拟和间接模拟.
直接模拟是指模拟模型的变量与原现象的变量之间存在一一对应的关系. 例如,用电系统模拟热传导系统,那么静电容量、电阻、电压、电流分别与热容量、热阻、温压、热流量相对 㡺. 由于电系统的参数容易测量和改变, 经常用电系统来模拟机械、热学等各种现象和过程.
间接模拟模型的变量与原现象之间不能建立一一对应的关系. 虽然如此, 但有时间接模型却能非常巧妙地解决一些复杂问题. 下面举所谓斯坦纳 (Steiner) 问题为例, 设有若干个工 地, 为解决相互间的交通问题, 将在工地之间修建公路, 问线路如何选择使公路的总长度最少, 参见右图.
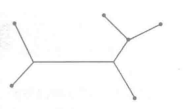
用其他的方法来解决是比较麻烦的, 我们可以采用如下的办法模拟. 将几个钉子按照工地之间的距离成比例地钉在木板上,代表各个工地,再将这块带钉子的木板浸入肥皂液中,然后细心地提出液面, 肥皂膜将联结在钉间, 由于肥皂膜要取其势能最小的形状,所以使联结在各钉间的肥莫膜总长度最小.
像这样的例子还有不少, 如将某范围的地面画在质量均匀的板 上, 再沿边界切开, 可用称地图板的质量的办法,按此例计算该范围的面积.
缩尺模型是将真实事物按比例缩小或放大的复制品, 如飞机模型和风洞是飞机在空中飞行的缩尺模型, 船舶模型和水槽是船舶在水中行驶的缩尺模型; 在模型实验, 化工工艺过程的化学实验等都是缩尺模型. 在科技工程中使用缩尺模型还是比较多的. 它的优点是对于许多复杂的现象, 当很难建立它的精确数学模型进行理论上的分析计算, 也找不到适当的模拟模型,而实物又太大或太小,无法直接实验时,采用缩尺模型进行实验是合适的.
这种缩尺 模型分享原实物的许多性质: 它可能有相同的外貌, 同样的颜色, 惎至和所表示的物体有类 似的功能. 例如, 模型帆船能漂浮并能靠风力推进, 由于缩尺模型并不具有 “母本” 实物的所有性质, 因而这种模型操作方便或能确切控制, 原物体的大小、质量等特征会妨碍我们对实 物进行工作, 而缩尺模型则易于掌握, 在操纵和研究模型中, 可以获得关于母本实物的信息, 例如,可用风洞中的模型飞机来决定超音速客机的航空特征,若造一架大小一样的飞机并在 风洞中进行测试的办法的代价是惊人的,因而缩尺模型在许多技术领域和工业研究中是一种很有价值的工具. 但是采用缩尺模型也存在不少问题, 如这种方法还是相当费时间、人力、 财力, 按缩尺模型得到的结果也不一定就是原实物或现象的结论, 其结果还要利用相似理论加以处理,这是很麻烦的.
理论模型既可以是实物、现象、过程的抽象表示形式, 也可以是我们所要描述的对象以及分析它们行为方式的抽象表示形式.一个物体、一种现像、某一过程的理论模型是观察者心目中确切表示该物体,现象、过程的一组规则和定律. 例如, 对土木工程师来说, 获得在荷载下的梁的挠度 (弯曲) 是重要的. 人们可以选一根梁加以荷载并测量其挠度,但这样做费时又费钱. 如果有一个荷载下梁的理论模型将更为方便. 经过实验、观察和计算, 就可以得出这种理论模型, 即 $$ \text { 挠度 }=\frac{P L^3}{48 E I} $$ 其中
- L 梁的长度;
- P 荷载;
- E 与梁的材料有关的弹性模量;
- I 与梁的横截面积有关的惯性矩. 在上述例子中, 挠度的模型 (理论模型) 是一个公式. 实际上,大多数重要的公式就是描述的现象的理论模型, 因而在科学研究和解决各实际问题中, 理论模型是不可缺少的工具.
数学模型
例如, 上述的挠度模型就是一个数学模型. 因此, 数学模型是关于部分现实世界和为一种特 殊目的而做的一个抽象的、简化的、近似表达对象的一种数学结构.
具体说来, 数学模型就是为了某种需要或目的, 用字母、数子字及其他数学符号建立起来的诸如等式或不等式, 以及图表、图像、框图等描述客观事物的特征及其内在联系的数学结构表达形式.
由于数学模型是针对或参照某种事物系统的主要特征、主要关系, 用形式化的数学语言,抽象概括地、简化近似地表述出来的一种数学结构,所以, 从广义上来说,数学模型是从现实世界中抽象出来,对客㷋事物的某些数学属性的一个近似反映. 例如众所周知的哥尼斯堡七桥问题便是大数学家欧拉成功地构造出数学模型得以解决的光辉例子. 如果从狭义上来理解,数学模型是由现实问題基本属性抽象出来成为一种数学结构的简化近似反映.
例 1 考虑两个物体之间的相互作用时, 对于它们之间的相互吸引这种属性, 可用数学式子 (即牛顿万有引力公式) $$ F=k \frac{m_1 m_2}{r^2} $$ 来表示吸引力与其他因素之间的规律, 这就是物质相互吸引的数学模型. 这个数学模型及其 理论是基于大量天文观测数据, 由牛顿在 17 世纪创立的, 它解决了大量天文学中的问题.
例 2 一个线性弹簧, 考察它的形变 x 与弹力 F之间的关系, 也可用数学式子 (胡克定理) $$ F=-K x $$ 来表示它们之间的规律, 负号表示形变的方向与弹力方向相反. 这个数学式子就是它的数学 模型. 这个模型表示了物理学中的一条重要规律.
一个系统是指按着一定方式互相连接起来的元素的集合. 一个系统范围的决定主要取决于我们研究的范围、目的和任务.一般把不属于系统的部分称为环境, 从环境向该系统 动的信息称为输人, 反之从系统向环境流动的信息称为输出. 建立一个系统的数学模型, 一般来说是要建立系统输入输出之间的关系式. 有时也将所关心的状态变量包含在数学模型之内. 要指出的是一个系统的数学模型不是唯一的, 要求的近似程度不同, 数学模型也有所不同.
由上可见, 对于同一个系统, 根据情况和要求的精确度不同,可有不同的数学模型. 任何数学模型都有现实原型(所反映的客观对象), 其原型可以是非数学的具体对象及 其性质、关系, 也可以是具体的数学对象及其性质、关系. 由于数学模型是数学抽象化的产物, 因而数学模型是它所模拟的具体对象的性质、关系的抽象, 这就可以使得数学模型本身有严格的逻辑结构. 对一个数学模型建立一套逻辑系统, 就得到相应的数学理论.
例4 自然数 0,1,2,3, ..., n, ...是最简单的数学模型. 自然数是从现实生活中抽象出来的数学概念. 在人类的众多种语言中不约而同地都有自然数出现, 可是总有一些数目, 由于很大, 而在语言中没有名称. 自然界的具体事物, 不管其数量有多大 (如沙子、米粒等), 总是一个有限数 (虽然这个数字, 我们没法确切给出), 而自然数这个模型不仅能表示很大的数, 而且还含有无穷大概念, 所谓“自然数结构”, 指的是定义了普通的自然数相等关系、小于关系、加法与乘法的自然数集合所形成的数学模型, 将逻辑运用于此数学模型, 就得到自然数理论. 正如大家所熟知的, 它给出了素数、合数概念, 除 0 与 1 以外的自然数可以表示为素数的乘积,素数有无穷多个, 等等, 当然,这个理论还给出了众多有趣的事实. 所有这些事实, 都是客观事物某些属性的反映.
例5 欧氏几何也是一个数学模型. 古希腊的《儿何原本》是按定义、公设、公理、定理 的逻辑结构将直线、三角形、圆等几何图形组织成有机的系统,详尽地推导他们的性质, 它的 基本图形都是现实生活中一些具体图形(如拉直的绳子、田地的形状等) 的抽象.
由上, 数学模型从表现形式上看大致可分为数式模型和图形 (包括逻辑结构图) 模型两种.
数式模型是系统的某种特征的本质的数学表达式, 即用数学式子(如函数式、代数方程 (组)、不等式(组)、微分方程(组)、差分方程(组)、微积分方程(组) 等) 来描述(表示、模 拟) 所研究的客贸对象或系统在某一方面的存在规律.
图形模型是用一些图形, 如逻辑结构图、方框图、流程图、状态迁移图、数表图等来表示所研究的现象、过程或理论的某种特征、属性或结构. 例如, 用地图来表示地理位置, 等高线图表示地面的高程,铁路线路图表示铁路连接状态,等等.
总而言之, 无论哪一种模型, 它都是对真实现象的一种近似表述; 而且只是表达真实现象某些方面的特征或属性. 即根据我们的目的, 从真实现象中选一部分所关心的特征或属性来进行描述,其他方面的特征将不予考虑, 对于其他的一些特性, 实际情况与模型甚至可以相差很远. 例如,一般地图, 它是大地的一种模型, 它保持各地区之间的距离和位置不变. 铁路线路示意图也是大地的一种模型,它只表示铁路线的联结情况,并不保持各点间的距离不变, 即是说这种示意图保持拓扑性质不变. 这两种模型是人们为了不同的目的, 对大地的不同属性所做的不同的近似描述.
- 沈文选、杨清桃 《数学建模尝试》
数学建模流程
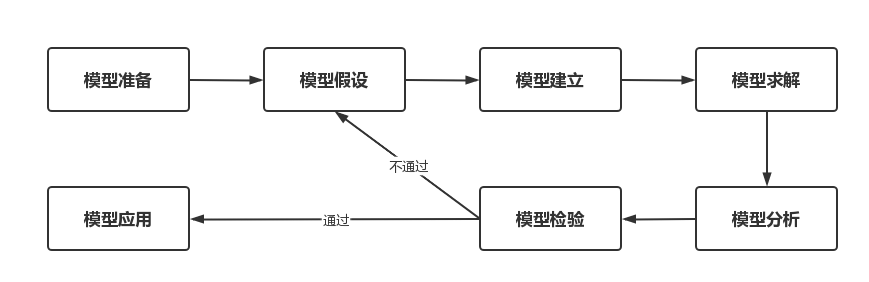
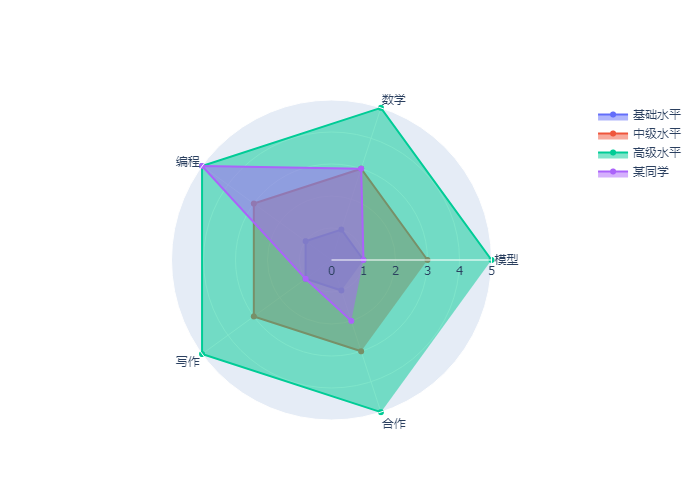
数学建模能力-五维度分析
数学建模能力是一项综合能力,我们可以从五个角度分析学生的数学建模能力:
数学能力 - 初中数学、高中数学、高等数学
建模能力 - 初等模型、重要高等模型、高阶高等模型
编程能力 - 基础编程、重要第三方库使用、高阶第三方库使用
写作能力 - 一般学术论文写作能力、特定数学模型写作能力、综合写作能力
合作能力 - 单人、双人、多人
最终我们希望学生的数学建模各方面能力都得到提升,而非仅是某些单项能力。
为什么要参加数学建模比赛

参考资料
Mathematical Models
An Introduction to Mathematical Modelling

我认为数学建模是解决日常问题的一种方式,通过建立模型的方式以数学思维看待问题,从而获得不同的思路和合理的结果。数学建模不仅是一种工具,也更是拓宽我们思维的优秀途径
首先数学建模的最终目标一定是解决实际问题。在我的认知中,首先是理论部分,其次是数据类型以及算法的模拟,最后是论文部分。当然,不可或缺的还有团队合作。总体来说,是一个锻炼多方面能力的项目。
数学建模指对一个实际问题进行数据收集、数据分析、问题分析、写作表达等步骤,用数学的逻辑或语言解决问题
数学模型就是对实际问题的一种数学表述。 具体一点说:数学模型是关于部分现实世界为某种目的的一个抽象的简化的数学结构。 更确切地说:数学模型就是对于一个特定的对象为了一个特定目标,根据特有的内在规律,做出一些必要的简化假设,运用适当的数学工具,得到的一个数学结构。数学结构可以是数学公式,算法、表格、图示等。
数学建模就是建立数学模型,建立数学模型的过程就是数学建模的过程