数学模型的分类
现实生活中的问题多种多样,从提问的方式上可以分为“是什么”“为什么”“怎么做”等;从提问的内容上可以分为“寻求现象解释”“获得最优方案”“预测未来变化”等; 从所需要的工具上来分可以涉及数学中各个分支的应用如几何、代数等;从现象上分可以分为确定性现象、不确定现象和模糊现象等。 本网站内容划分的原则综合考虑了上述因素,以问题目标和解决工具作为主要的分类依据,提出如下分类方法。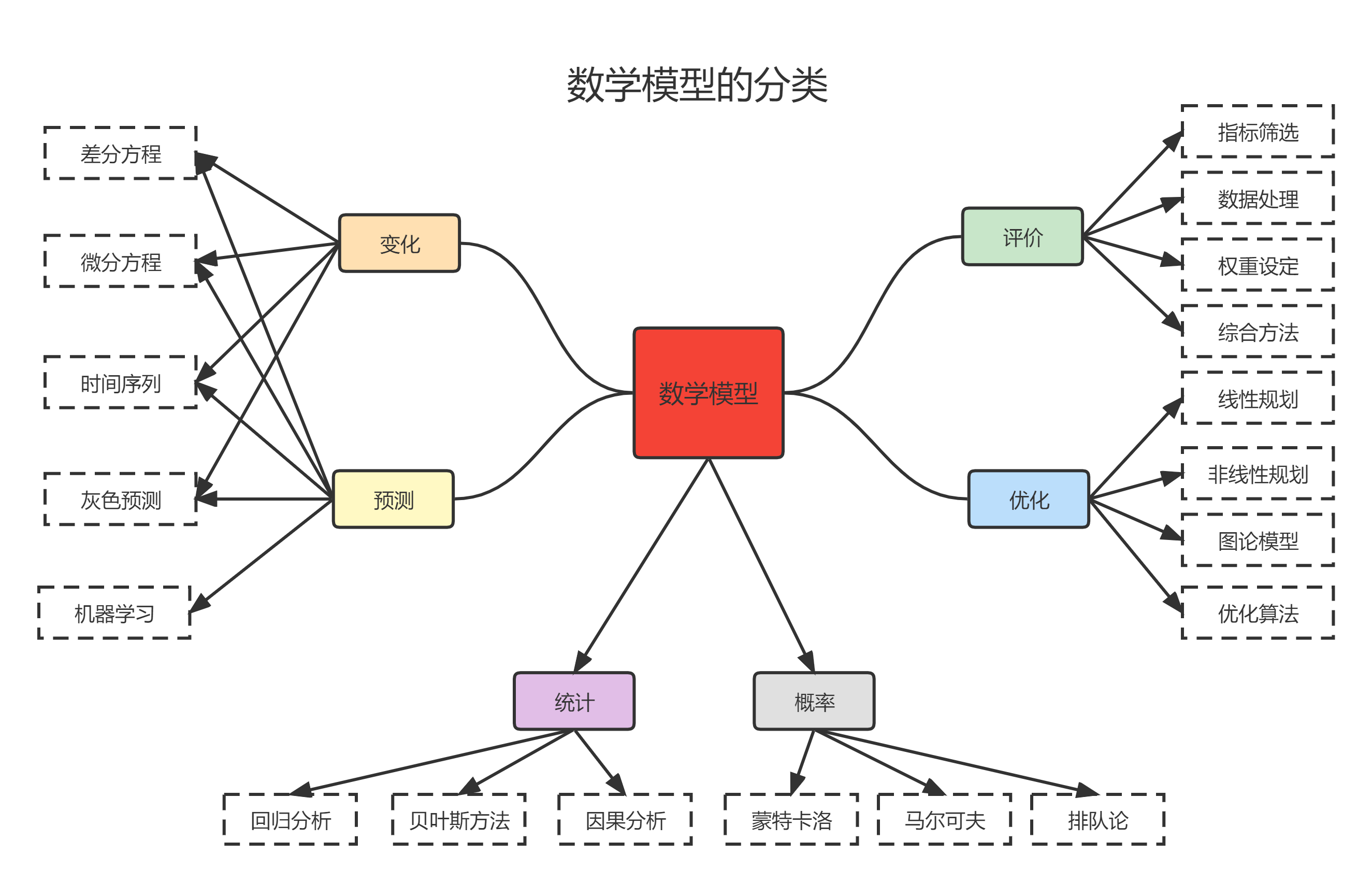
学生在学习过程中也会形成自己的分类法,这里提供的分类仅是体现了笔者习惯的分类和内容组织。 在笔者的分类体系下,相应的课件等资源也被分门别类的存放在如下页面:
- 初等模型包含量纲分析、比例建模以及一些使用初等数学知识解决的问题
- 评价模型包含评价体系的构成、归一化方法以及综合评价方法(如TOPSIS方法)
- 优化模型包含线性规划、非线性规划、启发式算法、图论、博弈论等内容
- 变化模型包含微分方程、差分方程等内容
- 预测模型包含机器学习方法、插值和拟合方法及时间序列模型等
- 统计模型包含聚类降维算法、回归理论等
- 概率模型包含排队论、蒙特卡洛模拟等
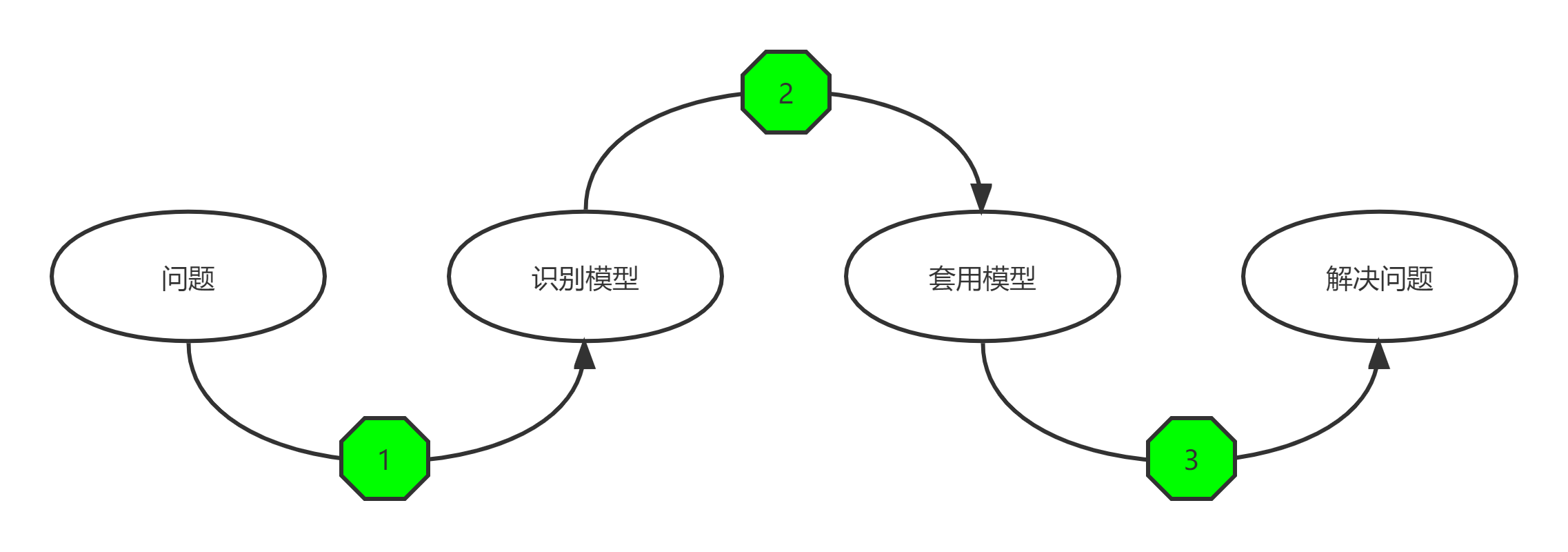
运用数学模型
数学建模的基本素养之一是能识别并套用模型解决问题。首先我们需要将复杂的问题情境进行提炼,指出该情境下解决问题的目标和方向是什么, 然后针对目标从记忆库或外部资源中提取合适的数学模型,接下来“套用”数学模型解决问题。这种解决问题的过程比较常见, 要求建模者熟悉常见的数学模型并了解模型的应用, 考验的是建模知识的理论基础和识别数学模型的能力。相比与前两者,求解倒是相对次要的一项了。