变化模型
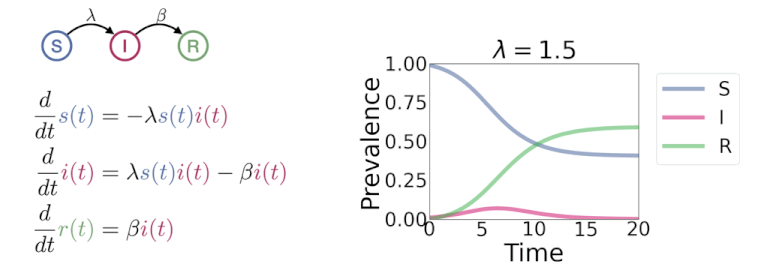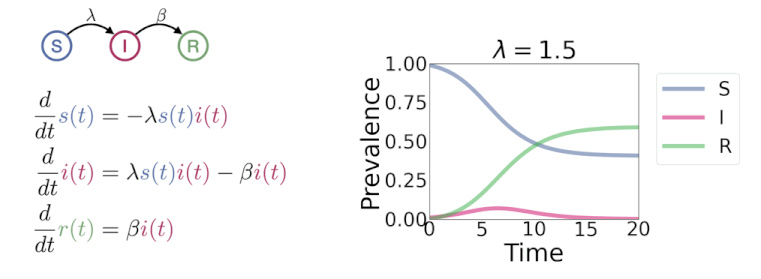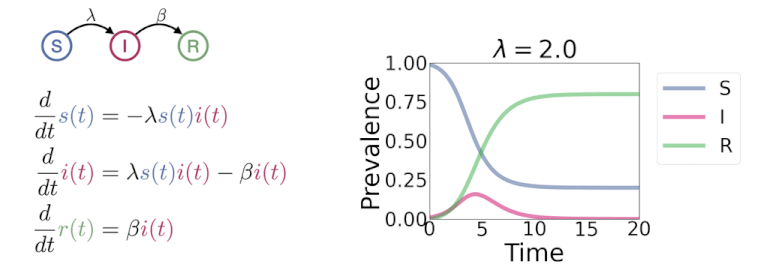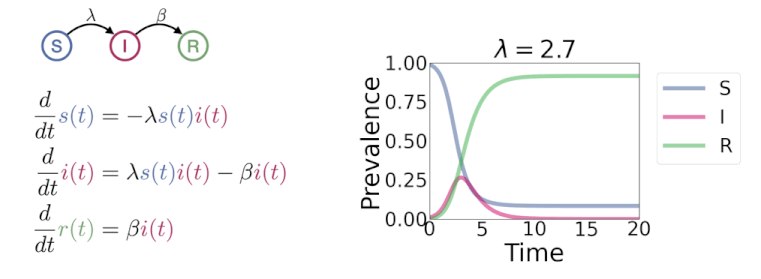
动态变化(dynamics)模型是刻画事物随时间而变化的模型,主要运用的工具有差分方程模型、微分方程模型, 以及时间序列等模型。解决动态变化的问题可以从机理和数据两个角度去解决。借助微积分从局部到整体的想法, 建模者可以通过对变化的观察(微分)获得对整体的宏观认识(函数)。差分方程适用于离散变化的情况,也可以用作对连续变化(微分)的近似。 时间序列模型主要从数据的角度寻求最佳的拟合规律来描述变化。
下面是近些年HiMCM中涉及到动态变化模型的赛题:
- 2012年A题 American Elk,濒危物种在新栖息地的繁衍
- 2014年B题 The Next Plague? 疫情处置
- 2018年B题 Cozy Smart House,温控系统的设计和调节
- 2019年B题 Bottle Battles,探讨瓶装水禁令可能带来的影响
微分方程
常微分方程(ODE)是一个包含一个或多个自变量的函数和这些函数的导数的微分方程。 “Ordinary”一词是与“偏微分方程”中"partial"一词相对的,偏微分方程可以是关于一个以上的自变量。
自学课件
- 如何用模型刻画战争走势|微信版
- 人口模型|微信版
- 传染病模型|微信版 🌿 SI,SIR,SEIR动态变化图
- 微分方程-药物在体内的分布|微信版
- 微分方程-种群的相互竞争
- 捕食者模型|微信版
- 微分方程的Python符号解|微信版
- 微分方程的Python数值解|微信版
- 微分方程建模方法-物体冷却|微信版
- 微分方程建模方法-微元分析法|微信版
- 微分方程建模方法-模拟近似法|微信版
差分方程
自学课件
- 差分方程-差分方程的稳定性|微信版
- 差分方程-Leslie方程|微信版
- 差分方程-养殖场问题|微信版
- 差分方程-减肥问题|微信版
- 差分方程-离散阻滞增长模型|微信版
- 差分方程-酵母菌增长|微信版
- 差分方程-染色体遗传模型|微信版
论文资源
新冠疫情期间,很多学者采用微分方程模型研究传染病的传播规律,并给予探寻到的传播规律进行预测和政策评估。 下文列出一些近期发表的论文供大家参考:
- A comparison of five epidemiological models for transmission of SARS-CoV-2 in India
- Analysis and Prediction of COVID-19 Using SIR, SEIQR, and Machine Learning Models Australia, Italy, and UK Cases
- COVID-19 Risk Estimation using a Time-varying SIR-model
- Ebola Epidermic in West Africa Using SIR Model that uses ODEs and PRDs
- Measuring and Preventing COVID-19 Using the SIR Model and Machine Learning in Smart Health Care
- Modeling Epidemics With Compartmental Models
- SIR model for assessing the impact of the advent of Omicron and mitigating measures on infection pressure and hospitalization needs
- TW‑SIR time‑window based SIR
- Verification of the accuracy of the SIR model in forecasting based on the improved SIR model with a constant ratio of recovery to infection rate by comparing with monitored second wave data
